P á g i n a 1 | 7. Regla de Simpson 1/3, Aplicación Simple (2 segmentos) Recuerde que la Regla de Simpson 1/3 es para número de segmentos pares.. Ejemplo 1. Con la ecuación de la Regla de Simpson 1/3 (ecuación anterior) , integre. Regla de Simpson: fórmula, demostración , ejemplos, ejercicios. La regla de Simpson es un método para calcular, en forma aproximada, las integrales definidas. Se fundamenta en dividir el intervalo de integración en un número par de sub-intervalos igualmente espaciados. Los valores extremos de dos sub-intervalos consecutivos definen tres.
Método de simpson 1/3 ejercicios resueltos YouTube
PPT Regla de Simpson 1/3 simple PowerPoint Presentation ID3187108
Metodo de Simpson 1/3 Matlab YouTube
PPT Regla de Simpson 1/3 simple PowerPoint Presentation ID3187108
Ejercicio Resuelto Con Metodo de Simpson 1/3 PDF
MÉTODO DE SIMPSON 1/3 PARA INTEGRALES CÓDIGO VBA/EXCEL YouTube
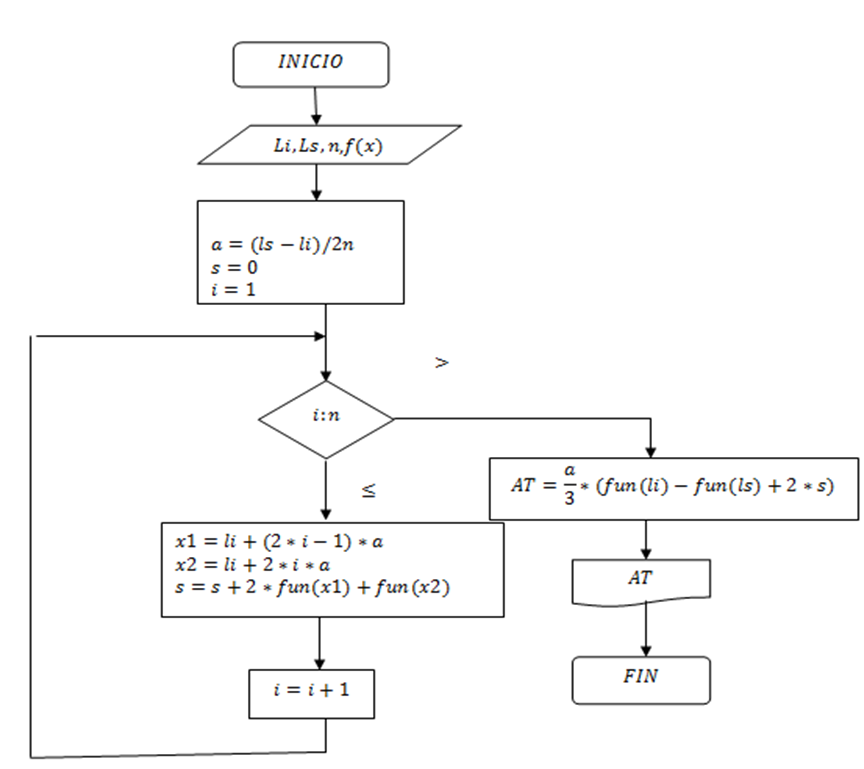
El blog de Jair Beltrán Algoritmo integración numérica, Simpson 1/3 (un tercio) Numerical
📏 Regla de Simpson 1/3 de aplicación múltiple en MATLAB YouTube
PPT Regla de Simpson 1/3 simple PowerPoint Presentation, free download ID3187108
Demostración regla de Simpson 1/3 YouTube
Cálculo numérico integração numérica regra 1/3 de Simpson. YouTube
6.8. Método de Simpson 1/3 YouTube
![Numerical Methods Simpsons 1/3rd rule [updated] YouTube](https://i.ytimg.com/vi/AamSY0Naly0/maxresdefault.jpg "Numerical Methods Simpsons 1/3rd rule [updated] YouTube")
Numerical Methods Simpsons 1/3rd rule [updated] YouTube
Integração Numérica Regra 1/3 Simpson + Scilab YouTube
PPT Regla de Simpson 1/3 simple PowerPoint Presentation ID3187108
PPT Regla de Simpson 1/3 simple PowerPoint Presentation, free download ID3187108
Simpson 1/3
Método de Simpson 1/3 YouTube
Método de Simpson 1 3 OCTAVE PDF Integral Escalar (Matemáticas)
Metode Simpson 1/3 YouTube
Alonso Ramírez Manzanares Métodos Numéricos 13.10.2014 Integración Numérica. Regla de Simpson. MAT-251 Dr. Alonso Ramírez Manzanares. Regla de Simpson. La función f ( x) (azul) es aproximada por una función cuadrática P ( x) (rojo). En análisis numérico, la regla o método de Simpson (nombrada así en honor de Thomas Simpson) y a veces llamada regla de Kepler es un método de integración numérica que se utiliza para obtener la aproximación de la integral : .
